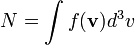
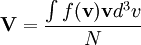
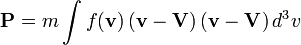
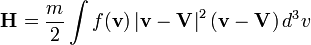
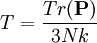
This is a generic tool for manipulating a particle Phase Space
Density. It provides the capability to take a slice through the
distribution normal to an arbitrary vector as well as computing
the usual moments of particle distributions: density, bulk
velocity, pressure tensor, heat flux and temperature. It permits
the user to specify a spacecraft potential and an energy cut off
for moments calculation. It can also find the PSD values along a
vector and convert the PSD into velocity space.
It is largely based on "Paschmann, G, AN Fazakerley, and SJ Schwartz: Moments of plasma velocity distributions, Analysis Methods for Multi-spacecraft Data, ISSI Scientific Report SR-001, 1998." Sets of parameters allow tuning the computation depending on the properties of the plasma and of the spacecraft.
It has been tested successfully by comparing its results to
those produced by the PEACE and CIS teams on some arbitrarily
chosen events.
You may contact the QSAS team at: qsassupp@gmail.com.
The input data set as a time series of arrays. The data must be
convertible to Joules ("SI_CONVERSION" attribute), and the
coordinates system must be spherical (either latitude or
co-latitude for the polar angle). The tool itself will determine
which of the dimensions are the angle and energy coordinates.
The "ENTITY" attribute, if present, is used to determine the
mass and charge of the particle, but these may also be manually
selected.
There is an intrinsic ambiguity in the definition of Phase Space Density due to the possibility that the radial coordinate is given in terms of the flow direction or look direction. Note that for Cluster CIS uses Flow direction, whilst PEACE uses Look direction. This tool sets the measurement direction parity automatically when either PEACE of CIS data are dropped into the PSD data slot, but this must be set manually for other data sets.
The Input PSD is usually in a local Spacecraft frame. On Cluster,
PEACE uses SR2 while CIS uses ISR2 (which is close to GSE). To
provide the output in a scientifically useful frame it is
necessary to provide the spacecraft spin axis latitude and
longitude in either GSE or GSM. The default is to assume GSE
unless the Coordinate_System or Frame attribute is provided and
set to GSM.
Alternatively, it is possible to provide a rotation matrix from
the Data coordinate system to the target coordinate system.
The user can choose the output to be in either GSE or GSM (irrespective of the frame of Spacecraft axis Latitude and Longitude) or an arbitrary frame determined by the input rotation matrix.
It is possible to generate and save only
the rotation matrix from Data frame to chosen output frame
for later use in this tool or elsewhere.
This is used to compensate for the effect of the particle
acceleration in the vicinity of the spacecraft. The potential is
converted to energy by multiplying it with the particle's charge.
This value is subtracted from the energies in the distribution.
Any resulting negative energies are discarded.It may be supplied
as a numerical value in volts, or as a data object with a valid
SI_conversion attribute. The default is to assume volts.
The potential must be a non-negative value.
Energies under this threshold are discarded (applied before potential correction). This can be used to remove the effect of photoelectrons. No correction is done to compensate for the removal of this data. It may be provided as a numerical value in eV or as a data object with valid SI_conversion. The default is to assume eV.
The moments of the PSD in the selected coordinate system after
taking account of the Spacecraft potential and selected lower
energy cut off. It is possible to select all provided moments or
just a selected subset using the tick boxes. The default is to
generate only the density.
This returns a two dimensional cartesian or polar slice through
the PSD, normal to a specified direction. It is possible to
specify the number of bins required in (each dimension of) the
array. The default result is in velocity space with axes binned in
velocity and the slice in units of per velocity cubed, however, an
option to return the slice in energy is provided. The x and y axes
in the slice can be controlled by the choice of selection of the
normal, see below.
Options are controlled by the following inputs:
This returns a gyro-phase averaged pitch angle distribution as a
2D array in polar coordinates, taking as inputs the velocity-space
origin from which to calculate pitch angles and the field
direction. User input includes the number of energy bins, pitch
angle bins, and also the number of gyrophase cuts, equally spaced
in phi, used to perform the average.
Let E be an energy value. If E is lower than the photoelectron threshold, nothing is done. Else, E'=E+P.C, where P is the non-negative potential of the spacecraft and C the signed charge of the particle.
If E' is non-negative, it is converted into velocity v, knowing that 2E'=mv.v (m for the particle mass) and knowing the measuring probe coordinates (and the GSE transformation matrix).
If f is the distribution function, the computed moments are:
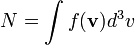
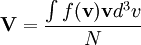
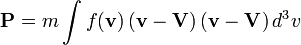
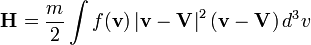
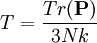
This method is the faster of the two, it is also the most naive one. It simply consists in the sum of the elementary integrations over the bin volumes, simply approximated by multiplying the data values over the bin volumes.
In the following illustrations, the principles are shown on a
partial coverage of a 2D plane. The data values are shown as red
shades, and the bin boundaries are dashed lines.
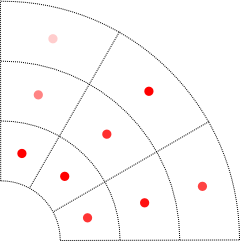
A part of the 2D plane is segmented into bins, each one carrying a value.
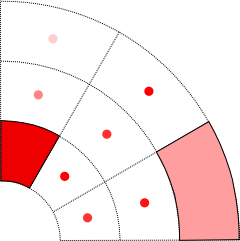
As illustrated on two bins, the integrated value is the value multiplied by the bin volume. These values are summed to give the total integrated result.
Despite its speed, this method is flawed when the data is sparse, as gaps are not filled.